Bài 1: Một khúc sông rộng lớn 20m. Một chiếc thuyền qua sông bị dòng nước đẩy xiên nên phải chèo 26m bắt đầu sang được bờ mặt kia. Hỏi làn nước đã đẩy mẫu thuyền lệch đi một góc bao nhiêu? (góc làm tròn mang lại độ)

Bài 2: Một máy cất cánh từ mặt đất gồm đường cất cánh lên chế tác với mặt đất một góc 300. Hỏi sau khi bay được 10km thì khoảng cách của dòng sản phẩm bay với mặt khu đất là bao nhiêu?
Bài 3: Một cột đèn cao 7m có bóng trên mặt đất nhiều năm 4m. Hãy tính góc (làm tròn mang lại độ) mà tia sáng khía cạnh trời tạo với mặt đất.
Bạn đang xem: Bài toán thực tế hình học lớp 9
Bài 4: Một cây cao 3 m. Ở 1 thời điểm vào ban ngày mặt trời chiếu sản xuất thành bóng lâu năm 2 m. Hỏi dịp đó góc tạo bởi tia sáng phương diện trời cùng mặt khu đất là từng nào ? (làm tròn số đo góc tới độ).
Bài 5: một cái thang dài 3m ghi:“ nhằm đảm bảo bình an khi dùng, phải kê thang cùng với mặt khu đất một góc tự 600 cho 700“. Đo góc thì khó khăn hơn đo độ dài. Vậy hãy cho biết thêm :khi dùng thang đó chân thang phải kê cách tường khoảng tầm bao nhiêu mét để bảo đảm an toàn an toàn? (làm tròn 2 chữ số thập phân)
Bài 6: Tính độ cao của một cây cổ thụ có bóng cùng bề mặt đất nhiều năm 8m và bao gồm tia sáng sủa từ đỉnh tạo thành với mặt đất một góc bằng 600
Bài 7: Một chiếc máy bay bay lên với gia tốc 500km/h. Đường bay lên sản xuất với phương nằm ngang một góc

Bài 8: Một người mong muốn làm một mái bịt cho một cửa sổ, tính tự tường ra khoảng 1mét, nghiên xuống 30 độ so với khía cạnh đất. Hỏi tín đồ đó yêu cầu cắt miếng tôn dài từng nào mét ? ( hiệu quả làm tròn chữ số thập phân thứ 2)
Bài 9: Vào buổi trưa, trơn của toà công ty in trên mặt đất nhiều năm 16m. Tính độ cao của toà nhà kia biết góc tạo vì chưng tia nắng và mặt khu đất là 500.
Bài 10: Tính chiều cao của một ngôi nhà tất cả bóng trên mặt đất nhiều năm 3m và gồm tia sáng sủa từ đỉnh tạo thành với mặt đất một góc bằng 600.
Bài 11: hải đăng Đá Lát là một trong những trong bảy ngọn hải đăng cao nhất Việt Nam, được bỏ trên đảo Đá Lát tại phần cực Tây quần đảo, nằm trong xã đảo Trường Sa, thị xã Trường Sa, tỉnh giấc Khánh Hòa. Ngọn hải đăng được xuất bản năm 1994, cao 42m, có tính năng chỉ địa chỉ đảo, giúp tàu thuyền hoạt động trong vùng biển cả Trường Sa định hướng và xác minh được địa chỉ của mình. Một tín đồ đi tàu trên biển muốn mang đến hải đăng Đá Lát, người đó đứng bên trên mũi tàu và cần sử dụng giác kế đo được góc thân mũi tàu và tia ánh nắng phản chiếu từ đỉnh ngọn hải đăng mang lại tàu là 100.
a/ Tính khoảng cách từ tàu mang lại ngọn hải đăng. (Làm tròn cho một chữ số thập phân).
b/ bên trên tàu còn 1 lít dầu, cứ đi 10m thì tàu kia hao tốn không còn 0,02 lít dầu. Hỏi tàu đó gồm đủ dầu để đến ngọn đèn biển Đá Lát tuyệt không? do sao? bài 12: Tính chiều cao của một ngọn núi cho thấy tại hai điểm cách nhau 1km cùng bề mặt đất người ta thấy được đỉnh núi với góc nâng theo thứ tự là 40o với 32o.


Bài 13: Từ bên trên tháp quan tiếp giáp của một ngọn hải đăng cao 28m, bạn ta nhìn thấy một cái thuyền cứu nạn với góc hạ 20o. Tính khoảng cách từ chân tháp cho thuyền.
Bài 14: Một người dân có mắt bí quyết mặt khu đất 1,4m, đứng giải pháp tháp Eiffel 400m thấy được đỉnh tháp cùng với góc nâng 39o. Tính độ cao của tháp ( có tác dụng tròn mang đến mép ).

Bài 15: nhị ngư dân đứng ở bên một bờ sông cách nhau 250m cùng nhìn thấy một xoay lao bên trên sông với các góc nâng theo lần lượt là 30o với 40o. Tính khoảng cách d từ bờ sông đến quay lao.

Bài 16: Một bức tượng cao 1,6m được để lên 1 mẫu bệ. Tại một điểm trên mặt đất người ta nhận thấy nóc tượng và nóc bệ với các góc nâng theo thứ tự 60o với 45o. Tính độ cao của dòng bệ.
Bài 17: Để đo chiều rộng lớn AB của một con sông mà chưa phải băng ngang qua nó, một bạn đi từ bỏ A đến C đo được AC = 50m với từ C nhận thấy B với cùng một góc nghiệng 62o với bờ sông. Tính chiều rộng của bé sông


Bài 18: nhị trụ điện cùng độ cao được dựng thẳng đứng phía 2 bên lề đối lập một quốc lộ rộng 80m. Từ một điểm M bên trên mặt mặt đường giữa nhị trụ tín đồ ta bắt gặp đỉnh hai trụ năng lượng điện với các góc nâng theo lần lượt là 60o cùng 30o. Tính chiều cao của trụ điện và khoảng cách từ điểm M cho gốc mỗi trụ điện.

Bài 19: một chiếc tháp được mặt bờ một nhỏ sông, xuất phát điểm từ 1 điểm đối diện với tháp ngay bờ bên kia bạn ta thấy được đỉnh tháp với góc nâng 60o. Từ một điểm khác cách điểm ban sơ 20m tín đồ ta cũng thấy được đỉnh tháp cùng với góc nâng 30o. Tính độ cao của tháp và bề rộng của sông
- Chọn bài bác -Bài 1: một vài hệ thức về cạnh và con đường cao trong tam giác vuôngBài 2: Tỉ con số giác của góc nhọn
Bài 3: Bảng lượng giác
Bài 4: một số trong những hệ thức về cạnh cùng góc trong tam giác vuông
Bài 5: Ứng dụng thực tế các tỉ con số giác của góc nhọn
Ôn tập chương 1
Xem toàn cục tài liệu Lớp 9: tại đây
Sách Giải Sách bài bác Tập Toán 9 bài 5: Ứng dụng thực tế các tỉ số lượng giác của góc nhọn giúp cho bạn giải những bài tập trong sách bài bác tập toán, học tốt toán 9 để giúp đỡ bạn rèn luyện khả năng suy luận hợp lý và phải chăng và đúng theo logic, hình thành kỹ năng vận dụng kết thức toán học vào đời sống cùng vào những môn học khác:
Bài 72 trang 117 Sách bài bác tập Toán 9 Tập 1: bài toán cái thangThang AB lâu năm 6,7m tựa vào tường có tác dụng thành góc 63o với khía cạnh đất. Hỏi độ cao của dòng thang đã đạt được so với phương diện đất?
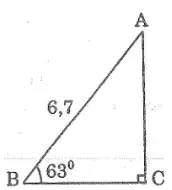
Lời giải:
Chiều cao của thang là cạnh góc vuông đối diện với góc 63o.
Ta có: AC = AB.sin
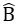
Vậy chiều cao của loại thang có được so với mặt đất là 6m.
Bài 73 trang 117 Sách bài bác tập Toán 9 Tập 1: Bài toán cột cờLàm dây kéo cờ: kiếm tìm chiều lâu năm của dây kéo cờ, biết nhẵn của cột cờ (chiếu vị ánh sánh khía cạnh trời) lâu năm 11,6m và mắt nhìn mặt trời là 36o50’
Lời giải:
Chiều cao của cột cờ là cạnh góc vuông đối diện với góc 36o50’, bóng cột cờ là cạnh kề với góc nhọn.
Chiều cao cột cờ là: 11,6.tg36o50’ ≈ 8,69 (m)
Chiều nhiều năm dây kéo cờ gấp rất nhiều lần cột cờ: 2.8,69 = 17,38 (m)
Chiều cao của cột cờ là cạnh góc vuông đối lập với góc 36o50’, nhẵn cột cờ là cạnh kề với góc nhọn.
Chiều cao cột cờ là: 11,6.tg36o50’ ≈ 8,69 (m)
Chiều lâu năm dây kéo cờ gấp hai cột cờ: 2.8,69 = 17,38 (m)
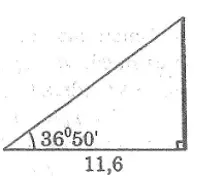
Bài 74 trang 118 Sách bài xích tập Toán 9 Tập 1: Bài toán nhỏ mèoMột conmèo nghỉ ngơi trên cây cỏ cao 6,5m. Để bắt mèo xuống cần phải đặt thang thế nào cho đầu thang đạt độ dài đó, khi đó góc của thang so với mặt đất là bao nhiêu, biết cái thang nhiều năm 6,7m?
Lời giải:
Độ cao của bé mèo chính là cạnh góc vuông đối diện với góc tạo do cái thang với mặt đất, chiều lâu năm thang là cạnh huyền.
Ta có: sin β = 6,5/6,7 ≈ 0,9701
Suy ra: β ≈ 75o57’
Vậy góc của thang đối với mặt đất là 75o57’
Bài 75 trang 118 Sách bài bác tập Toán 9 Tập 1: Bài toán đài quan sátĐài quan ngay cạnh ở Toronto, Ontario, Canada cao 533m. Ở một thời điểm nào đó vào ban ngày, phương diện Trời chiếu chế tạo ra thành bóng nhiều năm 1100m. Hỏi lúc đó góc tạo vày tia sáng khía cạnh trời với mặt đất là bao nhiêu?
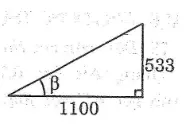
Lời giải:
Chiều cao của đài quan cạnh bên là cạnh góc vuông đối lập với góc nhọn, bóng của chính nó trên mặt đất là cạnh góc vuông kề với góc nhọn
Ta có: tg β = 533/1100 ≈ 0,4845
Suy ra: β ≈ 25o51’
Vậy góc tạo vị tia sáng mặt trời cùng mặt đất là 25o51’
Bài 76 trang 118 Sách bài xích tập Toán 9 Tập 1: Bài toán đèn biểnMột người xem ở đài đèn biển cao 80 feet (đơn vị đo lường và tính toán Anh) so với mặt nước biển, chú ý một loại tàu sinh sống xa cùng với góc 0o42’. Hỏi khoảng cách từ tàu đến chân đèn biển tính theo đơn vị hải lí là bao nhiêu? (1 hải lí = 5280 feet) (hình dưới)
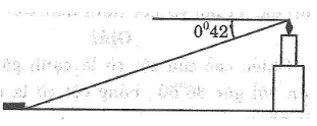
Lời giải:
Chiều cao ngọn hải đăng là cạnh góc vuông đối diện với góc 0o42’, khoảng cách từ tàu cho chân ngọn hải đăng là cạnh kề với góc nhọn.
Vậy khoảng cách từ tàu mang đến chân ngọn đèn biển là:
80.cotg0o42’ ≈ 6547,76 (feet) ≈ 1,24 (hải lí)
Bài 77 trang 118 Sách bài xích tập Toán 9 Tập 1: Bài toán máy bay hạ cánhMột máy cất cánh đang cất cánh ở chiều cao 10km. Khi bay hạ cánh xuống mặt đất, đường đi của sản phẩm bay chế tạo ra một góc nghiêng so với phương diện đất.
a. Nếu như phi công mong muốn tạo góc nghiêng 3o thì cách sân bay bao nhiêu ki-lô-mét phải bước đầu cho máy bay hạ cánh?
b. Ví như cách sân bay 300km, thứ bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu?
Lời giải:
a. Độ cao của sản phẩm bay là cạnh góc vuông đối diện với góc 3o, khoảng cách từ máy cất cánh đến sân bay là cạnh huyền
Vậy khoảng cách từ máy cất cánh đến trường bay là:
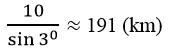
b. Ta có: sin β = 10/300 = 1/30
Suy ra: β ≈ 1o55’
Vậy khi trang bị bay bước đầu hạ cánh thì góc nghiêng là 1055’
Bài 78 trang 118 Sách bài tập Toán 9 Tập 1: Bài toán chiếu xạ chữa bệnhMột khối u của một bệnh nhân cách mặt domain authority 5,7cm, được chiếu vì một chùm tia gamma. Để tránh làm cho tổn thương mô, bác bỏ sĩ đang đặt mối cung cấp tia giải pháp khối u (trên phương diện da) 8,3cm (hình bên)
a. Hỏi góc tạo vì chùm tia với mặt da?
b. Chùm tia nên đi một đoạn dài bao nhiêu để mang lại được khối u?
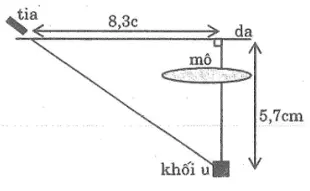
Lời giải:
a. Khoảng cách từ mặt da mang đến khối u là cạnh góc vuông đối lập với góc nhọn, khoảng cách từ chùm tia mang đến mặt da là cạnh kề.
Ta có: tg β = 5,7/8,3 ≈ 0,6867
Suy ra: β ≈ 34o29’
Vậy góc tạo do chùm tia với mặt domain authority là 34o29’
b. Đoạn mặt đường chùm tia đi cho khối u là:
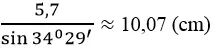
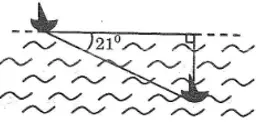
Tàu ngầm đã ở trên mặt biển khơi bỗng đột ngột lặn xuống theo phương tạo thành với mặt nước biển lớn một góc 21o (hình bên)
a. Giả dụ tàu vận động theo phương lặn xuống được 300m thì nó ở độ saau bao nhiêu? lúc đó khoảng cách theo phương nằm ngang so với nơi xuất hành là bao nhiêu?
b. Tàu cần chạy từng nào mét để đạt mang lại độ sâu 1000m?
Lời giải:
a. Độ sâu của tàu là cạnh góc vuông đối lập với góc 21o, phần đường đi của tàu là cạnh huyền, khoảng cách theo phương nằm ngang là cạnh kề của góc nhọn.
Độ sâu của tàu đạt được là: 300.sin21o ≈ 107,5 (m)
Khoảng cách từ tàu mang lại nơi khởi thủy là: 300.cos21o ≈ 280 (m)
b. Đoạn đường tàu đi được là:
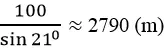
Lời giải:
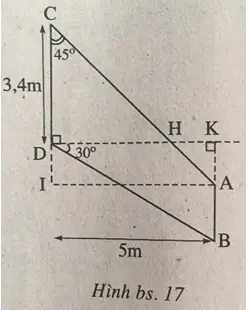
Đường thẳng AC cắt đường thẳng vuông góc với CD tại D sinh hoạt điểm H thì tam giác CDH là tam giác vuông cân, DH = CD = 3,4m. Đường trực tiếp AB cắt DH tại K thì DK = 5m buộc phải H nằm trong lòng D, K (xem h.bs.17).
Xem thêm: Tiết Lộ 14 Cách Làm Chân Thẳng Và Thon Và Thẳng Trong 1 Tuần Hiệu Quả #1
Dựng hình chữ nhật AKDI thì AIC là tam giác vuông cân, AI = KD = 5m cùng AC = AI√2 = 5√2 (m).