Logarit lớp 12 có rất nhiều kiến thức đặc trưng mà những em cần nắm rõ khi ôn luyện Toán trung học phổ thông thi đại học. Để giúp những em gồm cái nhìn rõ ràng về vùng kỹ năng này, cũng tương tự có kế hoạch ôn tập xuất sắc nhất, thuộc VUIHOC tra cứu hiểu cụ thể về logarit nhé!
Trước khi lấn sân vào bài viết, các em phát âm bảng bên dưới đây để sở hữu nhận định tầm thường về logarit lớp 12 vào đề thi
THPT nước nhà nhé:

Lý thuyết chung về logarit lớp 12 đã có thầy cô VUIHOC tổng thích hợp lại thành file tiếp sau đây giúp những em tiện lợi hơn vào ôn tập với theo dõi bài bác giảng:
Tải xuống file tổng hợp triết lý logarit lớp 12 không thiếu và đưa ra tiết
1. Khái quát kim chỉ nan chung về logarit lớp 12
1.1. Logarit là gì? những loại logarit trong chương trình log toán 12
Trong toán học, logarit của một số trong những là lũy thừa mà lại một giá trị ráng định, call là cơ số, đề nghị được nâng lên để tạo thành số đó. Có thể hiểu đơn giản, logarit chính là phép toán nghịch đảo của lũy thừa, hiểu một cách đơn giản hơn thì hàm logarit chính là đếm số lần lặp đi lặp lại của phép nhân.
Bạn đang xem: Giải bài tập toán 12 logarit
Ví dụ, logarit cơ số 10 của 1000 là 3 vị 1000 là 10 lũy vượt 3: 1000 = 10 × 10 × 10 = 103. Tổng quát hơn, nếu $x=b^y$ thì $y$ được gọi là logarit cơ số $b$ của $x$ cùng được ký hiệu là $log_bx$.
Có 3 loại logarit lớp 12:
Logarit thập phân: là logarit có cơ số 10, viết tắt là $log_10b=logb(=lgb)$có nhiều vận dụng trong công nghệ và kỹ thuật.
Logarit từ bỏ nhiên: là logarit tất cả cơ số là hằng số e, viết tắt là $ln(b)$, $log_e(b)$ có vận dụng nhiều vào toán học và vật lý, nhất là vi tích phân.
Logarit nhị phân: là logarit sử dụng cơ số 2, cam kết hiệu là $log_2b$ có áp dụng trong khoa học máy tính, lập trình ngôn từ C
Ngoài ra, ta còn 2 cách phân các loại khác là logarit phức (là hàm ngược của hàm lũy thừa trong các phức) cùng logarit rời rạc (ứng dụng vào mật mã hoá khoá công khai)
Tóm lại, công thức chung của logarit có dạng như sau:
Logarit gồm công thức là logab trong số đó $b>0$, $0
1.2. Bảng công thức logarit cơ bản
VUIHOC tổng hợp cho các em một số công thức loga cơ phiên bản dùng để chuyển đổi các phép tính logarit. Xung quanh ra, những công thức toán 12này rất đặc biệt vì nó cũng dùng làm ứng dụng trong các phép thay đổi hàm log.
Công thức tích, thương, luỹ thừa với căn:

Công thức thay đổi cơ số:
Logarit $log_bx$ rất có thể được tính từ logarit cơ số trung gian k của x cùng b theo công thức:

Các laptop bỏ túi nổi bật thường tính logarit cơ số 10 với e. Logarit cơ số b bất kỳ có thể được xác định bằng phương pháp đưa 1 trong hai logarit đặc biệt quan trọng này vào cách làm trên:

2. Dạng toán logarit lớp 12 cơ bản
2.1. Các dạng toán tương quan đến phương trình log toán 12
Dạng 1: phương thức đưa về thuộc cơ số giải logarit lớp 12
Một lưu giữ ý bé dại cho các em chính là trong quá trình thay đổi để kiếm tìm ra cách giải những bài tập log toán 12, họ thường quên việc kiểm soát miền khẳng định của phương trình. Vày vậy nhằm cho an toàn thì bên cạnh phương trình logarit cơ bản, chúng ta nên để điều kiện xác định cho phương trình trước lúc biến đổi.
Phương pháp giải dạng bài log toán 12 này như sau:
Trường đúng theo 1: $log_af(x)=b => f(x)=a^b$Trường đúng theo 2: $log_af(x)=log_ag(x)$khi và chỉ khi $f(x)=g(x)$Ta thuộc xét lấy một ví dụ sau để rõ hơn về cách áp dụng bí quyết giảilogarit lớp 12bằng cách đưa về cùng cơ số:

Dạng 2: Giải phương trình logarit lớp 12bằng giải pháp đặt ẩn phụ
Ở giải pháp giải bài tập log toán 12này, khi đặt ẩn phụ, chúng ta cần chăm chú xem miền giá trị của ẩn phụ nhằm đặt đk cho ẩn phụ hoặc không. Ta có công thức tổng thể như sau:
Phương trình dạng: $Q
Các em cùng VUIHOC xét lấy một ví dụ áp dụng phương pháp đặt ẩn phụ nhằm giải logarit lớp 12sau đây:

Dạng 3: nón hoá giải bài tậplogarit lớp 12
Bản chất của bài toán giải phương trình logarit cơ bạn dạng (ở trên) cũng là mũ hóa 2 vế với cơ số a. Trong một số trường hợp, phương trình gồm cả loga gồm cả mũ thì ta có thể thử vận dụng mũ hóa 2 vế nhằm giải.
Phương trình $log_af(x)=log_bg(x)(a>0, a eq 1)$
Ta đặt $log_af(x) = log_bg(x)=t$ => Hoặc $f(x)=a^t$ hoặc $g(x)=b^t$
=> Đưa về dạng phương trình ẩn $t$.

Dạng 4: bí quyết giải việc logarit lớp 12 bằng đồ thị
Giải phương trình: $log_ax=f(x)$ $(0
Bước 1: Vẽ thiết bị thị các hàm số: $y=log_ax(0
Bước 2: kết luận nghiệm của phương trình đã cho là số giao điểm của đồ vật thị
Ta tất cả ví dụ minh hoạ về phương pháp giải bài xích tập log toán 12 này như sau:


2.2. Những dạng toán về bất phương trình logarit
Dạng 1: Giải bất phương trình Logarit bằng phương pháp đưa về cùng cơ số
Lý thuyết bắt buộc nhớ:
- bí quyết để biến đổi bất phương trình logarit cơ bản về thuộc cơ số là:
$logaf(x)>logag(x)f(x)>g(x) (00; g(x)>0)$$logaf(x)>bf(x)>ab(00)$- Đặc biệt: Đối với các phương trình hoặc bất phương trình Logarit, ta luôn luôn phải nhớ đặt điều kiện để những biểu thức $log_af(x)$ bao gồm nghĩa. Rõ ràng là $f(x)>0$.
Ví dụ 1: $log_3(2x+1)>log_35$
ĐK: $2x+1>0Rightarrow x>-frac12$
Ta có: $log_3(2x+1)>log_35Rightarrow 2x+1>5Rightarrow 2x>4Rightarrow x>2$ (TMĐK)
Ví dụ 2: $log_2(x-5)+log_2(x+2)>3$
ĐK: $x-5>0$, $x+2>0Rightarrow x>5$
Ta có: $log_2(x-5)+log_2(x+2)>3Rightarrow log_2(x-5)(x+2)>3Rightarrow (x-5)(x+2)>2^3$
$Leftrightarrowx^2-3x-18>0$
$Leftrightarrow x6$
Kết phù hợp điều kiện: $x>6$.
Dạng 2: Giải bất phương trình Logarit bằng cách thức đặt ẩn phụ
Lý thuyết yêu cầu nhớ:
- với phương trình hoặc bất phương trình bao gồm dạng biểu thức logaf(x) thì ta hoàn toàn có thể đặt ẩn phụ theo hình thức $t=log_af(x)$.
- luôn phải đặt điều kiện để biểu thức $log_af(x)$ có nghĩa là $f(x)>0$.
- chú ý khi giải bất phương trình Logarit ta cần chăm chú đặc điểm của bất phương trình vẫn xét (có chứa dấu căn tuyệt không, gồm ẩn ở chủng loại hay không…) để lấy ra đk phù hợp.
Ví dụ 1: $4log_9x+logx_3-3>0$

Ví dụ 2: $1+log_2(x-1)>logx-14$

Dạng 3: bí quyết giảilogarit lớp 12cơ bản bằng phương pháp xét tính đối kháng điệu của hàm số.
Lý thuyết bắt buộc nhớ
- Trong một vài trường hợp ta cần yếu áp dụng phương thức đưa về thuộc cơ số hay để ẩn phụ nhằm giải bài xích tập logarit lớp 12thì ta hoàn toàn có thể sử dụng phương thức xét tính đối kháng điệu của hàm số.
- phương pháp này thường xuyên được sử dụng để giải bất phương trình logarit có nhiều cơ số không giống nhau.
- Để áp dụng phương thức này ta chỉ cần biến hóa bất phương trình về dạng hàm số rồi xét tính solo điệu với tìm ra nghiệm (hoặc tập nghiệm).

2.3. Những dạng toán liên quan đến hàm logarit
Dạng 1: kiếm tìm tập khẳng định của hàm số logarit
Đây là dạng cực kỳ cơ bản trong bài bác tập hàm số logarit. Khi tiến hành giải, các em dựa vào 2 luật lệ sau:
+ Hàm số $y=a^x$ cần điều kiện là a là số thực dương và $a$ không giống 1.
+ Hàm số $y = log_ax$ cần điều kiện:
• Số thực a dương với khác 1.
• $x>0$
Ví dụ minh hoạ:

Dạng 2: Tính đạo hàm của hàm số logarit
Ở dạng này, bọn họ vận dụng những công thức đạo hàm, đạo hàm logarit để thực hiện biến đổi. Chúng ta cùng xét lấy ví dụ như minh hoạ về một cách biến thay đổi tìm đạo hàm logarit sau:

Dạng 3: Ứng dụng đạo hàm vào khảo sát đồ thị hàm logarit
Đây là bước cải thiện hơn của các bài tập dạng 2, nghĩa là sau thời điểm tìm đạo hàm việc sẽ yêu mong thêm những em một bước nữa đấy là điều tra khảo sát và vẽ trang bị thị hàm số sẽ cho. Ở đây, họ áp dụng những kỹ năng về rất trị, giá trị lớn nhất, giá chỉ trị bé dại nhất… nhằm giải bài bác toán.
Để rõ hơn, ta thuộc xét lấy một ví dụ minh hoạ sau đây:


Dạng 4: rất trị hàm số logarit cùng min - max nhiều biến
Đây là dạng toán ở tầm mức độ áp dụng - vận dụng cao. Để giải được các bài tập cực trị của hàm số, các em buộc phải vận dụng xuất sắc các công thức biến hóa và nỗ lực chắc các đặc thù của hàm số logarit.
Cùng VUIHOC xét 2 ví dụ dưới đây để hiểu phương pháp làm dạng toán cực trị và min max này nhé!



3. Bài bác tập áp dụng
Để giải những bài tập log toán 12 cấp tốc và đúng đắn nhất, các em mua ngay bộ bài xích tập rèn luyện logarit mà những thầy cô VUIHOC đang soạn riêng bộ quà tặng kèm theo các em. Trong file này chứa đầy đủ các dạng bài xích tập logarit toán 12 từ cơ bạn dạng đến áp dụng cao, kèm giải cụ thể giúp những em hoàn toàn có thể tự ôn tập được sinh hoạt nhà. Cài đặt ngay theo link sau đây nhé!
Tải xuống file bài tập bất phương trìnhlogarit lớp 12 tất cả đáp án bỏ ra tiết
Tải xuống file bài tập hàm số logarit (có đáp án)
Các em đã thuộc VUIHOC ôn lại toàn thể lý thuyết về logarit và các bài tập nằm trong logarit lớp 12. Chúc các em luôn luôn vui học với học xuất sắc nhé!
- Chọn bài -Bài 1: Lũy thừaBài 2: Hàm số lũy thừa
Bài 3: Lôgarit
Bài 4: Hàm số mũ. Hàm số lôgarit
Bài 5: Phương trình mũ cùng phương trình lôgarit
Bài 6: Bất phương trình mũ với bất phương trình lôgarit
Bài ôn tập chương II
Xem toàn bộ tài liệu Lớp 12: tại đây
Sách giải toán 12 bài xích 3: Lôgarit giúp cho bạn giải những bài tập trong sách giáo khoa toán, học giỏi toán 12 sẽ giúp bạn rèn luyện khả năng suy luận phải chăng và hợp logic, hình thành năng lực vận dụng kết thức toán học tập vào đời sống với vào các môn học tập khác:
Trả lời thắc mắc Toán 12 Giải tích bài xích 3 trang 61: search x để:
a) 2x = 8;
b) 2x = 1/4;
c) 3x = 81;
d) 5x = 1/125.
Lời giải:
a) 2x = 8 ⇔ 2x = 23 ⇔ x = 3.
b) 2x = 1/4 ⇔ 2x = 2(-2) ⇔ x = -2.
c) 3x = 81 ⇔ 3x = 34 ⇔ x = 4.
d) 5x = 1/125 ⇔ 5x = 5(-3) ⇔ x = -3.
a) Tính log1/24, log31/27.
b) Có những số x, y nào nhằm 3x = 0, 2y = -3 hay là không ?
Lời giải:
a) log1/24 = -2, log31/27 = -3.
b) không tồn tại số x, y nào để 3x = 0, 2y = -3 vì chưng 3x > 0,2y > 0 với tất cả x, y.
Trả lời câu hỏi Toán 12 Giải tích bài 3 trang 62: Hãy chứng minh các tính chất trên
loga1 = logaa0 = 0
loga a = logaa1 = 1
Lời giải:
Ta có:
alogab = aα cùng với α = logab. Từ tư tưởng ta gồm aα = b phải alogab = aα = b.
Đặt logaaα = b. Theo định nghĩa aα = ab phải α = b. Vậy logaaα = b = α.
Lời giải:
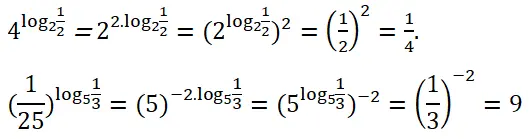
Trả lời câu hỏi Toán 12 Giải tích bài 3 trang 63: mang lại b1 = 23, b2 = 25.
Tính log2b1 + log2b2; log2b1b2 cùng so sánh các kết quả.
Lời giải:
log2b1 + log2b2 = log223 + log2 25 = 3 + 5 = 8.
log2b1b2) = log2(23.25 )= log2(2(3+5))= log2(28) = 8.
Vậy log2b1 + log2b2 = log2b1b2
Lời giải:
log1/22 + 2log1/21/3 + log1/23/8
= log1/22 + log1/21/3 + log1/21/3 + log1/23/8
= log1/2(2.1/3.1/3 .3/8) = log1/21/12.
Trả lời câu hỏi Toán 12 Giải tích bài 3 trang 64: đến b1 = 25, b2 = 23. Tính log2b1 – log2b2 , log2b1/b2 và so sánh những kết
Lời giải:
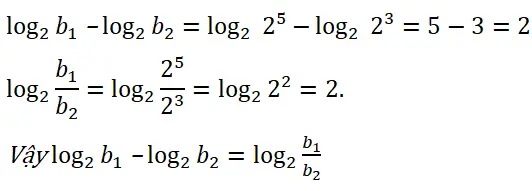
Tìm một hệ thức contact giữa ba tác dụng thu được.
Lời giải:
logab = log464 = log443 = 3.
Xem thêm: Quý cô lỡ thì - louis siu cheung yuen
logca = log24 = 2.
logcb = log264 = log226 = 6.
Vậy logcb = logca. Logab
Bài 1 (trang 68 SGK Giải tích 12): Không thực hiện máy tính, hãy tính: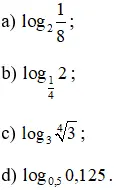
Lời giải:
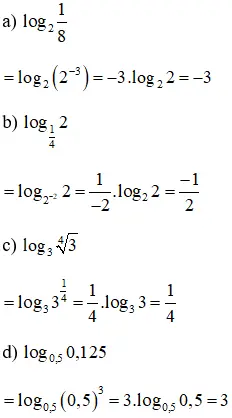
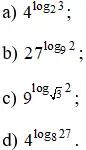
Lời giải:
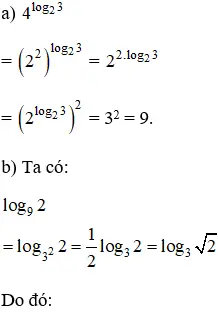
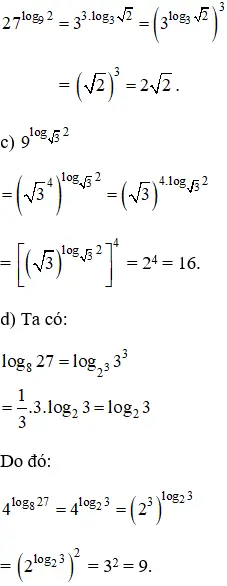
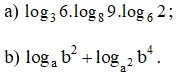
Lời giải:
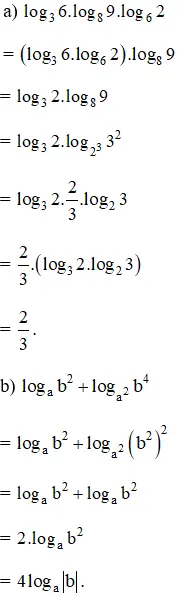

Lời giải:
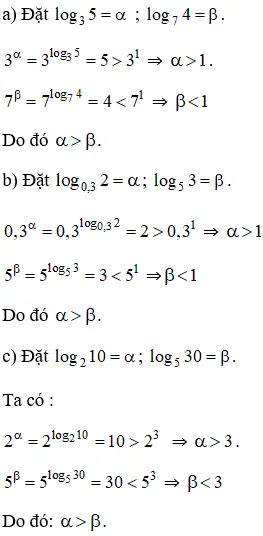
Hãy tính log301350 theo a, b.