Sinh viên các trường ĐH sau đây rất có thể học được bộ combo này:
- ĐH kinh tế tài chính Quốc Dân
- ĐH nước ngoài Thương
- ĐH yêu mến Mại
- học viện chuyên nghành Tài Chính
- học viện ngân hàng
- ĐH kinh tế tài chính Tp. Hồ Chí Minh
Chương trình học gồm những chương sau:
CHƯƠNG I - KHÔNG GIAN VÉCTƠ THỰC N CHIỀUBài 1: Hệ phương trình tuyến đường tính và phương thức khử ẩn liên tiếp(Phép khử Gauss)
Bài 2:Không gian véctơ thực n chiều
Bài 3: Độc lập đường tính và nhờ vào tuyến tính
Bài 4: các đại lý của không khí véctơ
Bài 5: Hạng của một hệ véctơ
CHƯƠNG II - MA TRẬN VÀ ĐỊNH THỨCBài 1: Ma trận
Bài 2: Định thức của ma trận và các đặc thù của định thức
Bài 3: Các phương pháp tính định thức của ma trận
Bài 4: Phép nhân ma trận với ma trận nghịch đảo
Bài 5: Ma trận nghịch đảo
Bài 6: Hạng của ma trận
CHƯƠNG III - HỆ PHƯƠNG TRÌNH TUYẾN TÍNH TỔNG QUÁTBài 1: Hệ phương trình Cramer
Bài 2: Hệ phương trình tuyến đường tính tổng quát
Bài 3: Hệ phương trình con đường tính thuần nhất
Bài 4: mô hình Input - đầu ra của Leontief
Bài 5: mô hình cân bằng thị phần và cân nặng bằng tài chính vĩ mô
CHƯƠNG IV - GIỚI THIỆU MỘT SỐ DẠNG ĐỀ THIĐề thi dứt học phần Toán cao cấp 1 cho những nhà tài chính - Đại số tuyến tính (Đề số 01)
Đề thi chấm dứt học phần Toán thời thượng 1 cho những nhà kinh tế tài chính - Đại số con đường tính (Đề số 02)
Đề thi chấm dứt học phần Toán thời thượng 1 cho những nhà tài chính - Đại số tuyến tính (Đề số 03)
Đề thi hoàn thành học phần Toán thời thượng 1 cho các nhà kinh tế - Đại số tuyến đường tính (Đề số 04)
Đề thi hoàn thành học phần Toán cao cấp 1 cho những nhà kinh tế - Đại số tuyến tính (Đề số 05)
Đề thi chấm dứt học phần Toán thời thượng 1 cho các nhà kinh tế - Đại số đường tính (Đề số 06)
Đề thi hoàn thành học phần Toán thời thượng 1 cho các nhà tài chính - Đại số con đường tính (Đề số 07)
Đề thi ngừng học phần Toán thời thượng 1 cho những nhà tài chính - Đại số tuyến tính (Đề số 08)
Đề thi ngừng học phần Toán cao cấp 1 cho những nhà kinh tế - Đại số tuyến tính (Đề số 09)
Đề thi dứt học phần Toán thời thượng 1 cho các nhà kinh tế - Đại số đường tính (Đề số 010)
Đề thi xong xuôi học phần Toán thời thượng 1 cho những nhà tài chính - Đại số đường tính (Đề số 011)
Đề thi xong học phần Toán cao cấp 1 cho các nhà kinh tế tài chính - Đại số đường tính (Đề số 012)
Xem chi tiết hơn tại mục lục khoá học bên dưới. So với một khối ngành kĩ thuật, khoá học này không bao gồm các chương Tập hợp, Logic, Số phức, Ánh xạ tuyến tính, Dạng toàn phương và Quy hoạc con đường tính.
Bạn đang xem: Toán cao cấp đại số tuyến tính
Hiện trên Vted.vn gây ra 2 khoá học Toán cao cấp 1 cùng Toán cao cấp 2 dành chosinh viên năm nhất hệ Cao đẳng, đại học khối ngành kinh tế tài chính của toàn bộ các trường:
Khoá học hỗ trợ đầy đủ kỹ năng và cách thức giải bài xích tập các dạng toán đi kèm theo mỗi bài bác học. Hệ thống bài tập rèn luyện dạng từ luận bao gồm lời giải cụ thể tại website để giúp đỡ học viên học cấp tốc và vận dụng chắc chắn kiến thức. Kim chỉ nam của khoá học góp học viên được điểm A thi cuối kì các học phần Toán cao cấp 1 cùng Toán thời thượng 2 trong số trường ghê tế.
Sinh viên các trường ĐH sau đây có thể học được bộ combo này:
- ĐH kinh tế Quốc Dân
- ĐH nước ngoài Thương
- ĐH thương Mại
- học viện Tài Chính
- học viện chuyên nghành ngân hàng
- ĐH tài chính ĐH tổ quốc Hà Nội
và những trường đại học, ngành tài chính của các trường ĐH khác trên mọi cả nước...
Trong công tác toán thời thượng môn đại số và hình giải tích, bài viết dưới shthcm.edu.vn sẽ share một số kiến thức cơ bạn dạng cùng với các dạng bài tập số phức toán cao cấp có giải thuật thường chạm mặt trong quá trình học.
1. Dạng bao gồm tắc số phức đại số đường tính
Định nghĩa số phức:
Số phức là sự kết hợp của số thực và số ảo. Số phức là các số được màn trình diễn dưới dạng a+bi, trong những số đó a,b là các số thực cùng i là số ảo được điện thoại tư vấn là “iota” .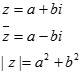
Ví dụ số phức: 1+i; 2+3i.
Một số ảo thường xuyên được biểu diễn bằng “i” hoặc “j” và bằng √-1. Do đó, bình phương của số ảo đến giá trị âm.
Vì, i = √-1, vì chưng đó, i 2 = -1
Bài học tập tiếp theo:
Các phép toán đại số trên số phức
Có tứ phép toán đại số số phức được liệt kê dưới đây.
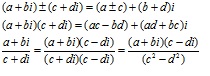
Xem bảng sau đây để phân biệt giữa số thực với số ảo.
| Số phức | Số thực | Số ảo |
| -1 + 2i | -1 | 2i |
| 7-9i | 7 | -9i |
| -6i | 0 | -6i (số ảo) |
| 6 | 6 | 0i (số thực) |
Modulus
Cho z = a + ib là một vài phức. Mô đun của z được màn biểu diễn bằng | z |.
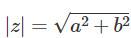
2. Dạng lượng giác của số phức
Tổng quát: z=r(cosφ + isinφ )Một số công thức về dạng lượng giác: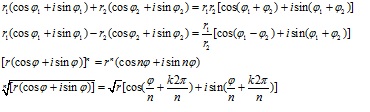
3. Giải bài bác tập số phức
Ví dụ: biến đổi các số phức sau thành dạng lượng giác(casio):Để giải số phức bằng cách đổi số phức quý phái dạng lượng giác casio ta thực hiện các bước sau:– đưa sang chính sách số phức với radian
– chọn OPTN > 1 r∠∅
Bài 1: Chuyển các số phức sau về dạng lượng giác
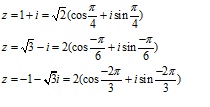
Bài 2: tra cứu căn bậc của những số phức sau
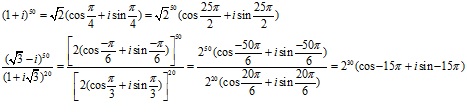
Bài 3:Tìm dạng lượng giác của các số phức sau:
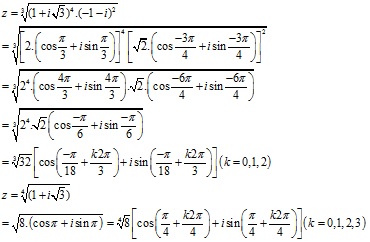
Tham khảo: bài bác tập chéo hoá tất cả lời giải
Bài 4: trình diễn hình học những số phức sau:
a / z1 = -1 + i
Điểm màn biểu diễn số phức z1=-1+i là (-1;1)
b / z2 = i
Điểm màn trình diễn số phức z2=i là (0;1)
c / z3 = 3
Điểm biểu diễn số phức z3=3 là (3;0)
Câu hỏi thường gặp mặt về số phức
0 có phải là số phức không?
Như họ đã biết, 0 là một vài thực. Và số thực là 1 phần của số phức. Do đó, 0 cũng là một trong những phức và hoàn toàn có thể được biểu diễn dưới dạng 0 + 0i.
Số phức có nghĩa là gì?
Số phức là sự phối kết hợp của một số thực và một số trong những ảo. Một lấy một ví dụ về số phức là 4 + 3i. Ở phía trên 4 là một vài thực với 3i là một số ảo.
Làm cầm cố nào nhằm chia những số phức?
Để phân tách số phức, hãy nhân tử số và chủng loại số với phối hợp của nó. Liên đúng theo của số phức hoàn toàn có thể được tìm thấy bằng cách đổi vết giữa nhị số hạng ở mẫu số. Sau đó, áp dụng phương pháp FOIL để đơn giản và dễ dàng hóa biểu thức.
Quy tắc tính số phức
Quy tắc số học của số phức là:Quy tắc cộng: (a + bi) + (c + di) = (a + c) + (b + d)i
Quy tắc trừ: (a + bi) – (c + di) = (ac) + (bd)i
Quy tắc nhân: (a + bi). (c + di) = (ac-bd) + (ad + bc)i
Viết ra đồng dạng cùng và nghịch hòn đảo của số phức.
Nhận dạng cùng của số phức được viết là (x + yi) + (0 + 0i) = x + yi. Do đó, danh tính cộng là 0 + 0i.Phép cộng nghịch hòn đảo của số phức được viết là (x + yi) + (-x-yi) = (0 + 0i). Do đó, nghịch hòn đảo của cộng là -x-yi.
Viết ra phép nhân với phép nghịch hòn đảo của số phức.
Xem thêm: Những Câu Nói Hay Về Sự Khinh Bỉ, Những Câu Nói Khinh Bỉ Hay Nhất
Nhận dạng nhân của số phức được quan niệm là (x + yi). (1 + 0i) = x + yi. Do đó, dấn dạng nhân là 1 trong những + 0i.Nhận dạng nhân của số phức được có mang là (x + yi). (1 / x + yi) = 1 + 0i. Do đó, phép nhân là 1 trong những / x + yi.