Bài viết cô sẽ hướng dẫn bạn cách vẽ đồ thị hàm số bậc nhất một cách đơn giản và chính xác nhất, và giới thiệu cách giải các dạng bài liên quan tới đồ thị hàm bậc nhất.
Bạn đang xem: Cách vẽ đồ thị hàm số bậc nhất
Cách vẽ đồ thị hàm sốCác dạng bài cơ bản về đồ thị hàm số bậc nhất:Vẽ đồ thị hàm số bậc nhấtTìm tọa độ giao điểm của hai đường thẳngXét tính đồng quy của ba đường thẳngTính khoảng cách từ gốc O đến đường thẳng không đi qua OTìm điểm cố định của đường thẳng phụ thuộc tham số
Nếu như ở bài trước bạn đã nắm được thế nào là hàm số bậc nhất thì ở bài này ta sẽ học cách vẽ đồ thị của hàm số bậc nhất. Điều bạn cần nhớ đầu tiên là:
Mục lục
ToggleCác dạng bài tập về đồ thị hàm số bậc nhất
Dạng 2: Tìm tọa độ giao điểm của hai đường thẳng.Dạng 3: Xét tính đồng quy của ba đường thẳng
Dạng 4. Tính khoảng cách từ gốc O đến đường thẳng (không qua O)Dạng 5. Tìm điểm cố định của đường thẳng phụ thuộc tham số
Đồ thị của hàm bậc nhất là một đường thẳng
Đồ thị của hàm số y = ax + b (a khác 0) là tập hợp các điểm trên tọa độ Oxy thỏa mãn phương trình y = ax + b.Kí hiệu:
Đường thẳng d: y = ax + b
Cách vẽ đồ thị của hàm số bậc nhất
Vì đồ thị của hàm bậc nhất là một đường thẳng nên ta chỉ cần tìm hai điểm thỏa mãn phương trình y = ax + b rồi nối chúng lại là xong.
1. Cách tìm điểm thỏa mãn hàm số bậc nhất y = ax + b:
Ta thay x = số rồi tính ra y thì sẽ tìm được 1 điểm.Ta có thể chọn các điểm đơn giản như x = 0 suy ra y = b, ta được điểm (x, b), x = 1 suy ra y = a + b thì ta được điểm (1, a+b).Cho y = 0 thì x = -b/a ta được điểm (-b/a, 0)2. Sau đó ta nối hai điểm lại thành một đường thẳng.
Vẽ đồ thị hàm số bậc nhất sau: y = 3x + 4.
Giải:
Trước tiên ta tìm hai điểm tọa độ (x,y) thỏa mãn y = 3x + 4.
Ta cho x = 0 thì y = 4.0 + 4 = 4, ta được điểm (0, 4).
Ta cho x = 1 thì y = 3.1 + 4 = 7, ta được điểm (1, 7).
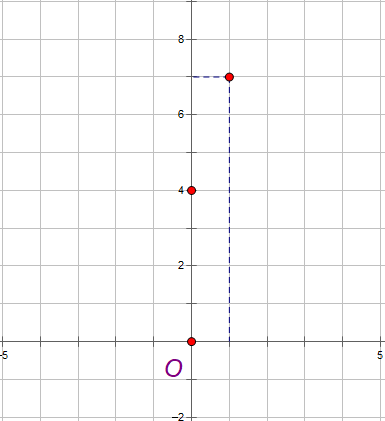
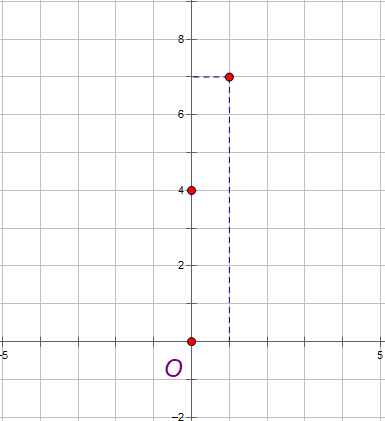
Xác định hai điểm vừa tìm được trên hệ trục tọa độ rồi ta nối chúng lại là xong.
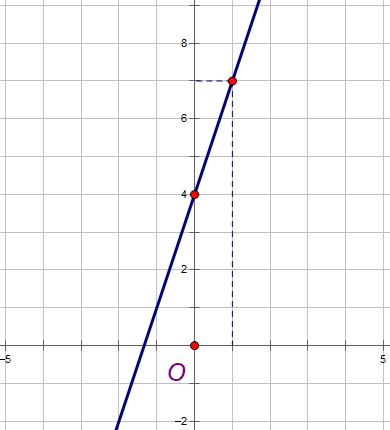
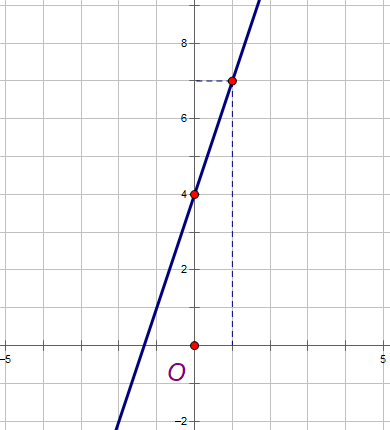
Chú ý rằng : y = 3x + 4 có a = 3 > 0 thì đồ thị có hướng lên trên từ trái sang phải.
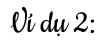
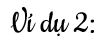
Vẽ đồ thị hàm số bậc nhất sau: y = -2x + 1.
Giải.
Ta chọn 2 điểm thỏa mãn y = -2x + 1:
+ Cho x = 0 suy ra y = 1, ta có điểm (0, 1).
+ Cho x = 1 suy ra y = -2 + 1 = -1, ta có điểm (1, -1).
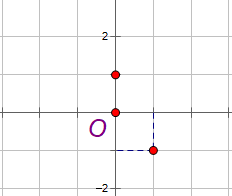
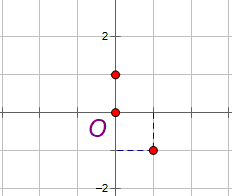
Sau đó ta nối hai điểm trên:
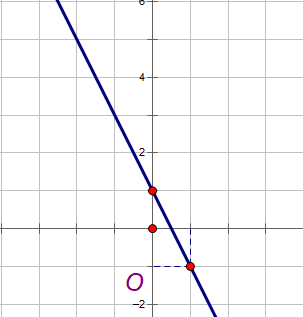
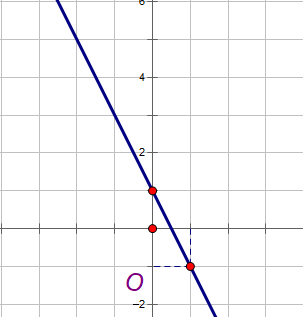
Chú ý rằng : y = -2x + 1 có a = -2 Các dạng bài tập về đồ thị hàm số bậc nhất
Dạng 1: Vẽ đồ thị hàm số bậc nhất
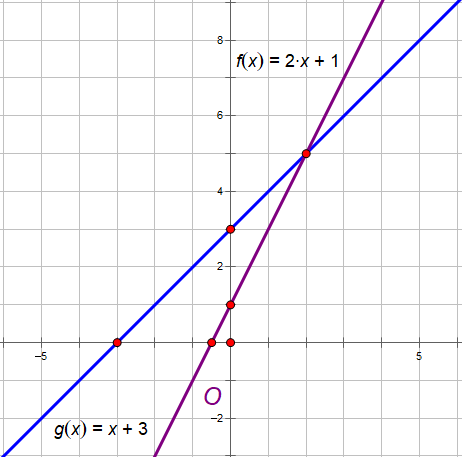
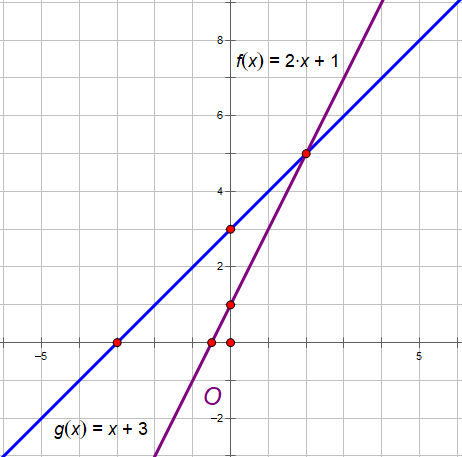
Vẽ các đồ thị hàm số bậc nhất sau trên cùng một mặt phẳng tọa độ:
y = 2x + 1 và y = x + 3
Giải.
Ta thực hiện hai bước như trên cô hướng dẫn:
+ Tìm 2 điểm thỏa mãn y = 2x + 1 rồi nối chúng lại. Ta được đường màu tím.
+ Tìm 2 điểm thỏa mãn y = x + 3 rồi nối chúng lại. Ta được đường màu xanh.


Như ta thấy, hai đồ thị của hai hàm số trên cắt nhau tại một điểm (gọi là giao điểm).
Vậy làm thế nào để tìm được tọa độ của giao điểm đó.
Ta sẽ sang dạng thứ 2 ngay sau đây.
Dạng 2: Tìm tọa độ giao điểm của hai đường thẳng.
Ta biết rằng đường thẳng là đồ thị hàm số bậc nhất nên để tìm giao điểm của hai đường thẳng ta có cách làm sau:
Phương pháp giải: Cho 2 đường thẳng d: y = ax + b và d’: y = a’x + b’. Để tìm tọa độ giao điểm của d và d’ ta làm như sau:
Dùng phương pháp đại số:
#1. Giải phương trình hoành độ giao điểm của d và d’: ax + b = a’x + b’ để tìm x.
#2. Từ x thu được ta thay vào phương trình của d (hoặc d’) để tìm y.
#3. Kết luận tọa độ giao điểm của d và d’ là điểm (x, y) vừa tìm được.
Bây giờ, ta sẽ tìm tọa độ giao điểm của hai đường thẳng d: y = 2x + 1 và d’: y = x + 3 ở ví dụ 3 phần trước.
Ta sẽ thực hiện như sau:
Xét phương trình hoành độ giao điểm của d và d’:
2x + 1 = x + 3
⇔ 2x – x = 3 – 1 (chuyển vế đổi dấu)
⇔ x = 2
Ta thay x = 2 vào phương trình của d: y = 2x + 1 = 2.2 + 1 = 5.
Kết luận: Vậy tọa độ giao điểm của d và d’ là (2, 5).
Ví dụ 4.Tìm tọa độ giao điểm của các đường thẳng




Giải.
Ta xét phương trình hoành độ giao điểm của d và d’ là








Ta thay x = 2 vào phương trình của d’ ta được: y = -x +2 =-2 + 2 = 0.
Kết luận: Vậy tọa độ giao điểm của d và d’ là (2, 0).
Trên đây là dạng tìm giao điểm của hai đồ thị hàm số bậc nhất, tiếp theo đây là giao của 3 đồ thị hàm số bậc nhất.
Dạng 3: Xét tính đồng quy của ba đường thẳng
Ba đường thẳng đồng quy là 3 đường thẳng phân biệt cùng đi qua một điểm.
Để xét xem 3 đường thẳng đã cho có đồng quy không ta làm như sau:
Phương pháp giải:
#1. Tìm tọa độ giao điểm của hai trong 3 đường đã cho.
#2. Thay tọa độ giao điểm vừa tìm được vào phương trình đường còn lại.
Nếu điểm đó thuộc đường còn lại thì kết luận ba đường thẳng đã cho đồng quy.
Ví dụ 5.
Cho 3 đường thẳng:


Chứng minh 3 đường thẳng đã cho đồng quy.
(Sách củng cố và ôn luyện Toán 9)
Giải.
Ta sẽ tìm giao điểm của hai trong ba đường đã cho. Ví dụ ta chọn




Xét phương trình hoành độ giao điểm của




3x – 1 = x + 3
⇔ 3x – x = 3 + 1
⇔ 2x = 4
⇔ x = 2
Thay x = 2 vào phương trình của


Vậy tọa độ giao điểm của




Thay x = 2 vào phương trình đường thẳng


y = 4x – 3 = 4.2 – 3 = 8 – 3 = 5. Suy ra điểm (2,5) thuộc


Kết luận: Vậy 3 đường thẳng đã cho đồng quy.
Ví dụ 6.Cho ba đường thẳng:


Tìm m để ba đường thẳng


(Sách củng cố và ôn luyện Toán 9)
Giải.
Phương pháp vẫn là tìm tọa độ giao điểm của




Ta chọn tìm giao điểm của


Xét phương trình hoành độ giao điểm của


x – 4 = 2x + 3
⇔ x – 2x = 3 + 4
⇔ -x = 7 ⇔ x = -7.
Thay x = -7 vào phương trình


Vậy tọa độ giao điểm của


Để 3 đường thẳng đã cho đồng quy thì tọa độ giao điểm của




Thay tọa độ vừa tìm được vào phương trình


-11 = -7m + m + 1
⇔ -11 -1 = -6m
⇔ 6m = 12
⇔ m = 2.
Kết luận: Nếu m = 2 thì ba đường thẳng đã cho đồng quy.
Tiếp theo ta sang dạng bài liên quan đến đồ thị hàm số bậc nhất, đó là tính khoảng cách từ gốc tọa độ O đến một đường thẳng không đi qua O
Dạng 4. Tính khoảng cách từ gốc O đến đường thẳng (không qua O)
Phương pháp giải:
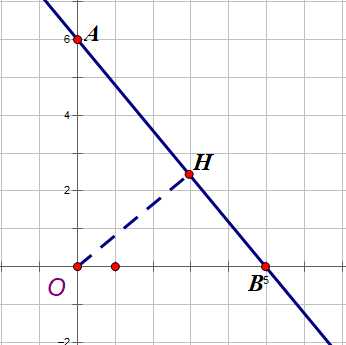
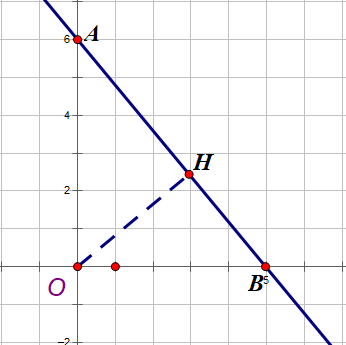
Để tính khoảng cách từ O đến đường thẳng d (không qua O) ta làm như sau:
#1. Tìm giao điểm của d với Oy và Ox lần lượt là A và B.
#2. Gọi H là hình chiếu của O trên d. Khi đó ta cần tính OH (chính là khoảng cách từ O đến d).
Áp dụng hệ thức lượng trong tam giác vuông, ta có


Ví dụ 7.
Trong hệ trục tọa độ Oxy, cho đường thẳng d: y = 2x + 5. Hãy tính khoảng cách từ gốc tọa độ O đến d.
Giải.
Đầu tiên ta vẽ đồ thị hàm số bậc nhất y = 2x + 5 tức là đường thẳng d.
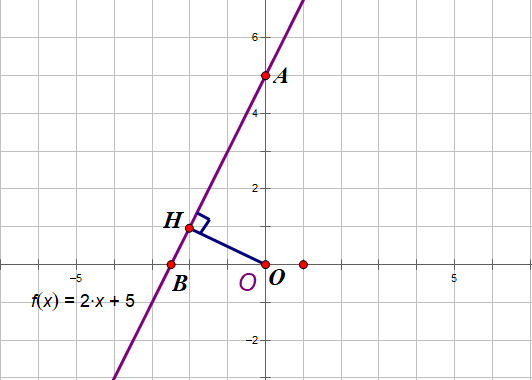
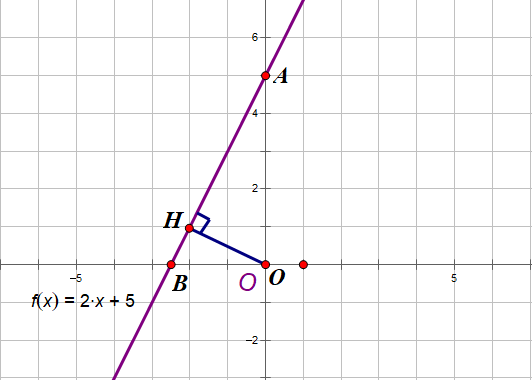
Điểm A là giao của d với Oy nên x = 0 và y = 2x + 5 = 2.0 + 5 = 5, vậy A(0,5)
Điểm B là giao của d với Ox nên y = 0 và 0 = 2x + 5 suy ra x = -5/2, vậy B(-5/2, 0)
Suy ra OA = 5, OB = 5/2. Gọi H là hình chiếu của O trên d. Ta tính OH dựa vào hệ thức lượng:




suy ra OH² = 5 ⇒ OH = √5.
Dạng bài tiếp theo liên quan đến đồ thị hàm số bậc nhất, đó là tìm điểm cố định của đường thẳng phụ thuộc tham số.
Tức là tìm tọa độ của điểm mà đồ thị hàm số bậc nhất luôn đi qua với mọi giá trị của tham số.
Dạng 5. Tìm điểm cố định của đường thẳng phụ thuộc tham số
Phương pháp giải:
Cho đường thẳng d: y = ax + b phụ thuộc tham số m.
Muốn tìm điểm cố định của đường thẳng d ta làm như sau:
#1. Gọi điểm cố định của d là F có tọa độ (x’, y’) suy ra y’ = ax’ + b với mọi m.
#2. Biến đổi y’ = ax’ + b về dạng hàm số bậc nhất hoặc bậc hai theo biến m.
Cho các hệ số của biến m bằng 0 rồi giải ra x’ và y’.
Ví dụ 8.
Cho đường thẳng d: y = (2m+1)x – 3m +1 với m là tham số.
Hãy tìm điểm cố định mà d luôn đi qua với mọi m.
Giải.
Gọi điểm cố định của d là F có tọa độ (x’, y’), ta có: y’ = (2m + 1)x’ – 3m + 1 với mọi m.
Ta viết lại như sau:
(2m + 1)x’ – 3m + 1 – y’ = 0 với mọi m
⇔ 2mx’ + x’ – 3m + 1 – y’ = 0 với mọi m
⇔ x’ = 3/2 và y’ = x’ + 1 = 3/2 + 1 = 5/2
Vậy tọa độ điểm cố định của đường thẳng d là F(3/2, 5/2).
Trên đây cô đã hướng dẫn các em các dạng toán đơn giản liên quan đến đồ thị hàm số bậc nhất, ngoài ra còn có hai dạng nâng cao hơn về đồ thị hàm số bậc nhất thì cô sẽ cập nhật sau đó là:
Tìm tham số m sao cho khoảng cách từ gốc tọa độ O đến đường thẳng cho trước là lớn nhất.Tìm tham số m sao cho đường thẳng cắt hai trục tọa độ tại hai điểm phân biệt tạo thành một tam giác thỏa mãn điều kiện cho trước.Như vậy, nhắc đến đường thẳng (đồ thị hàm số bậc nhất) thì ta sẽ sử dụng trực tiếp phương trình của hàm số bậc nhất một ẩn để giải các bài toán liên quan.
Đồ thị hàm số bậc nhất là một khái niệm cực kì quan trọng và cơ bản để chúng ta giải các bài toán về hàm số trong thi tuyển lớp 10. Vì thế chúng ta cần ôn luyện thật tốt về đồ thị hàm số bậc nhất, theo đó chuẩn bị kiến thức học về đồ thị hàm số bậc hai ở kì sau.
Bài viết này của shthcm.edu.vn sẽ mang đến cho các bạn tất cả các kiến thức tổng quan về hàm số bậc nhất. Bên cạnh đó là những dạng bài toán thường gặp trong các kì thi, đặc biệt là kì thi THPT Quốc Gia hằng năm.
1. Hàm số bậc nhất là gì?
Để giải được các bài toán về hàm bậc nhất, trước tiên các em cần nắm rõ định nghĩa và các công thức tính liên quan. Dưới đây, shthcm.edu.vn sẽ nêu rõ hàm số bậc nhất là gì và các công thức hàm số bậc nhất để các em ghi nhớ.
1.1 Lý thuyết hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b. Trong đó a, b là các số cho trước và a≠0. Và khi b = 0 hàm số bậc nhất có dạng y = ax, biểu thị tương quan tỉ lệ thuận giữa y và x.
Tính chất cần nhớ:
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có tính chất sau:
Đồng biến trên R nếu a>0
Nghịch biến trên R nếu a
1.2 Các dạng bài tập cơ bản thường gặp
Bài tập về hàm bậc nhất có 2 dạng cụ thể như sau:
Dạng 1: Xác định hàm số bậc nhất
Hàm số bậc nhất là hàm số có dạng y = ax + b (a≠0).
Ví dụ: Với điều kiện nào của m thì các hàm số nào sau đây là hàm số bậc nhất?
a) y = (m-1)x + m
b) y = (m2-2x -3)x2 + (m+1)x + m
c) y = √(m2-1).x + 2 .
Hướng dẫn giải:
a) y = (m-1)x + m là hàm số bậc nhất
y = (m-1)x + m &h
Arr; m – 1 ≠ 0 &h
Arr; m ≠ 1.
Vậy với mọi m ≠ 1 thì hàm số y = (m – 1)x + m là hàm số bậc nhất.
b) y = (m2-2x -3)x2 + (m+1)x + m là hàm số bậc nhất
y = (m2-2x -3)x2 + (m+1)x + m
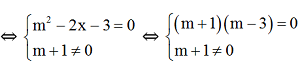
&h
Arr; m - 3 = 0 &h
Arr; m = 3
Vậy với m = 3 thì hàm số y = (m2-2x -3)x2 + (m+1)x + m là hàm số bậc nhất là hàm số bậc nhất.
c) y = √(m2-1).x + 2 là hàm số bậc nhất
&h
Arr; √(m2-1) ≠ 0 &h
Arr; m2 – 1 > 0 &h
Arr; m > 1 hoặc m 1 hoặc m
Đồng biến trên R nếu a>0
Nghịch biến trên R nếu a
Ví dụ: Tìm a để các hàm số dưới đây :
a) y = (a + 2)x + 3 đồng biến trên R.
b) y = (m2 – m).x + m nghịch biến trên R.
Hướng dẫn giải:
a) y = (a + 2)x + 3 đồng biến trên R
y = (a + 2)x + 3 &h
Arr; a + 2 > 0 &h
Arr; a > -2.
Vậy với mọi a > -2 thì hàm số y = (a + 2)x + 3 đồng biến trên R.
b) y = (m2 – m)x + m nghịch biến trên r
y = (m2 – m)x + m &h
Arr; m2 – m
2.2 Cách vẽ đồ thị hàm số bậc nhất
Trường hợp 1:Khi b = 0 thì y = ax là đường thẳng đi qua gốc tọa độ O(0;0) và điểm A (1;a) đã biết.
Trường hợp 2: Xét y = ax với a khác 0 và b khác 0.Ta đã biết đồ thị hàm số y = ax + b là một đường thẳng, do đó về nguyên tắc ta chỉ cần xác định được hai điểm phân biệt nào đó của đồ thị rồi vẽ đường thẳng qua hai điểm đó.
Cách thứ nhất:
Xác định hai điểm bất kỳ của đồ thị , chẳng hạn:
Cho x = 1 tính được y = a + b, ta có điểm A ( 1; a+b)
Cho x = -1 tính được y = -a + b, ta có điểm B (-1 ; -a + b)
Cách thứ hai:
Xác định giao điểm của đồ thị với hai trục tọa độ:
Cho x = 0 tính được y = b, ta được điểm C (-b/a;0)
Cho y = 0 tính được x = -b/a, ta có điểm D (-b/a; 0)
Vẽ đường thẳng qua A, B hoặc C, D ta được đồ thị của hàm số y = ax + b
Dạng đồ thị của hàm số y = ax + b ( a≠0)
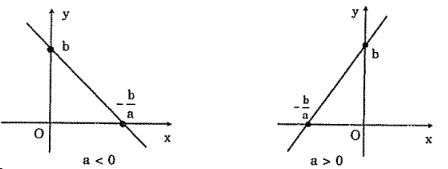
Ta cần xác định hai điểm phân biệt bất kì thuộc đồ thị.
Bước 1: Cho x = 0 => y = b. Ta được điểm P(0;b)∈Oy.
Cho y = 0 => x = −ba. Ta được Q(−ba;0)∈0x.
Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q, ta được đồ thị của hàm số y = ax + b.
2.3 Bài tập vẽ đồ thị hàm số thường gặp có lời giải
Bài tập 1: Vẽ đồ thị hàm số y = x + 2
Hướng dẫn giải:
Ta có:
x = 0 &r
Arr; y = 2
x = −1 &r
Arr; y =1
→ Đồ thị hàm số y = x + 2 đi qua 2 điểm (0;2) và (−1;1).
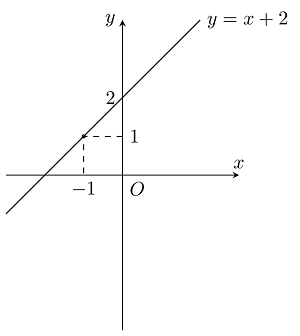
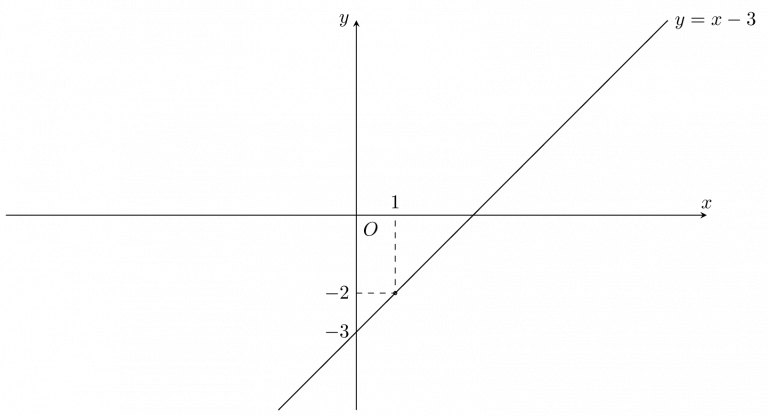
Bài tập 2: Vẽ đồ thị hàm số y = x − 3
Hướng dẫn giải:
Ta có:
x = 0 &r
Arr; y = −3
x= 3 &r
Arr; y = 0
→ Đồ thị hàm số y = x − 3 đi qua 2 điểm (0;−3) và (3;0).
Xem thêm: Những Câu Nói Hay Về Kỷ Niệm Tình Yêu Nhau Lãng Mạn # Top 15 View
Công thức tính diện tích hình vuông là gì? Bài tập và bí quyết thực hành hiệu quả
Cách tính bán kính hình tròn đơn giản và bài tập tự luyện hiệu quả
Chu vi hình tròn là gì? Công thức và bài tập vận dụng đầy đủ nhất
3. Sự biến thiên của hàm số bậc nhất
Một kiến thức quan trọng khác mà các em cần quan tâm khi học bài tập này đó chính là sự biến thiên của hàm số bậc nhất. Lý thuyết và cách giải bài tập về sựbiến thiên của hàm số bậc nhất cụ thể như sau:
3.1 Hàm số bậc nhất đồng biến và nghịch biến
Định nghĩa hàm số bậc nhất đồng biến khi nào? Và nghịch biến khi nào? Thường rất dễ bị nhầm lẫn trong quá trình ghi nhớ của các bạn học sinh. Nhất là những bạn học sinh cuối cấp và có rất nhiều công thức để ghi nhớ. Vậy, hãy cùng shthcm.edu.vn ôn lại định nghĩa về sự biến thiên của hàm số bậc nhất sau đây nhé!
Hàm số bậc nhất y = ax + b (a≠0) có tập xác định D = R, đồng biến trên R nếu a > 0 và nghịch biến trên R nếu a
Hàm số đồng biến a > 0 &h
Arr; 5 + k > 0 &h
Arr; k > -5
Hàm số nghịch biến a

Bài tập 2: Cho hàm số
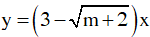
a, Hàm số đã cho là hàm bậc nhất
b, Hàm số đã cho đồng biến
c, Hàm số đã cho nghịch biến
Hướng dẫn giải:
Hàm số đã cho có hệ số a= 3 - √(m+2).
a, Hàm số đã cho là hàm bậc nhất &h
Arr; a ≠ 0 &h
Arr; 3 - √(m+2) ≠ 0 &h
Arr; √(m+2) ≠ 3
&h
Arr; m + 2 ≠ 9 &h
Arr; m ≠ 7
Vậy m ≠ 7
b, Hàm số đã cho đồng biến khi a > 0 ↔ 3 - √(m+2) > 0 &h
Arr; √(m+2) 3
&h
Arr; m + 2 >; 9 &h
Arr; m > 7
Vậy m > 7
Trên đây là tất cả kiến thức về hàm số bậc nhất mà shthcm.edu.vn đã tổng hợp giúp bạn. Hy vọng với những chia sẻ thực tế này, sẽ giúp bạn có một hành trang vững vàng hơn trong kì thi sắp tới. Xin được đồng hành cùng bạn!
Ba mẹ muốn con học giỏi môn Toán, đồng thời cải thiện khả năng ngôn ngữ tốt hơn thì đừng bỏ qua ứng dụng shthcm.edu.vn Math nhé!  |