Khi tiến hành tìm hiểu về các hàm lượng giác vào toán học chắc chắn chắn bạn sẽ nghe nói đến cosin – một hàm số vô cùng không còn xa lạ và sát cánh đồng hành cùng bạn trong số bài toán. Tuy nhiên có một số trong những bạn học sinh vẫn chưa nắm rõ về định lý hàm số cos và các ứng dụng phổ cập của nó đối với toán học. Bài viết sau đây CMath Education – Câu lạc cỗ toán học muôn color sẽ cùng chúng ta giải đáp các thắc mắc cùng hàm số này để giúp đỡ bạn học tập tập tốt hơn nhé.
Bạn đang xem: Định lý hàm cos trong vật lý
Sự thành lập và hoạt động của định lý hàm số cos
Định lý hàm số cos nghe bao gồm vẻ rất gần gũi nhưng không phải người nào cũng biết nó đến từ đâu được ra đời như vậy nào. Tiếp sau đây hãy cùng CMath tra cứu hiểu bắt đầu ra đời của hàm cosin nhé.
Về bên toán học Al Kashi
Định lý cosin là một trong những phần mở rộng của định lý Pitago. Nếu định lý Pitago cho họ một phương tiện hữu hiệu để tìm cạnh khuyết vào tam giác vuông thì định lý hàm số cosin hỗ trợ một phương pháp giúp kiếm tìm một cạnh của tam giác thông thường. Vào đó:
Các góc của tam giác khi biết cạnh của tam giácXác định cạnh thứ tía của tam giác nếu biết nhị cạnh và góc đối diện của 1 trong những hai cạnh này.
Định lý của Euclide
Vào vắt kỷ sản phẩm công nghệ III trước Công nguyên, có một định lý được phát biểu dưới kiểu dáng học bởi nhà toán học tập Euclide. Được xem như là tương đương với định lý hàm số cosin.
Định lý Euclide được tuyên bố như sau:
“Trong một tam giác tù, bình phương của cạnh đối lập góc tù to hơn so cùng với tổng bình phương của của nhị cạnh kề góc tù đọng là nhì lần diện tích s của hình chữ nhật bao gồm một cạnh bằng một trong hai cạnh kề góc tù hãm của tam giác (cụ thể là cạnh tất cả đường cao hạ xuống nó) cùng đoạn thẳng đã có cắt bớt từ đường thắng kéo dài của cạnh kia về phía góc tù do đường cao trên.”
Định lý hàm cosin vào tam giác
Hiểu và áp dụng định lý cosin thạo là điều kiện tiên quyết để các bạn học sinh đi sâu vào môn toán học. Để nắm vững được điều đó thì bọn họ hãy cùng đi tìm kiếm hiểu thực chất của định lý này nhé.
Phát biểu định lý cosin
Trong tam giác, ta phát biểu định lý cosin sau đây:
“Trong một tam giác phẳng, bình phương một cạnh bởi tổng bình phương nhì cạnh còn sót lại trừ đi nhì lần tích của chúng với cosin của góc xen thân hai cạnh đó.”
Công thức định lý hàm số cosin
Ta xét tam giác ABC bao gồm độ nhiều năm như sau: BC = a, AC = b, AB = c, các góc tương ứng: góc A = , góc B = , góc C = , ta có:

Nhận xét: trong một tam giác phẳng, nếu như biết nhì cạnh cùng góc xen giữa ta công thêm được độ lâu năm cạnh còn sót lại hoặc tính góc khi biết 3 cạnh của tam giác.
Trường hợp bao quát của định lý hàm số cosin là định lý Pitago.
Với cách làm trên, nếu tam giác ABC vuông thì ta có:
Tam giác ABC vuông trên A, cosa (A) = 0 → a2 = b2 + c2
Tam giác ABC vuông trên B, cosb (B) = 0 → b2 = a2 + c2
Tam giác ABC vuông trên C, cosy (C) = 0 → c2 = a2 + b2
Chứng minh định lý hàm số cos
Có nhiều cách để chứng minh định lý hoàn toàn có thể kể đến nhứ:
Sử dụng công thức tính khoảng tầm cáchSử dụng công thức lượng giác
Sử dụng định lý Pytago
Sử dụng định lý Ptolemy
Ở đây, để tiện lợi nhất ta nên sử dụng định lý Pytago, biện pháp làm vẫn như sau:
Xét tam giác ABC là tam giác nhọn, bao gồm BC = a, AC = b, AB = c, kė AH vuông góc cùng với BC trên H, AH = h, HC = d.

Xét tam giác vuông ABH, ta có:
h2 = c2-(a-d)2=c2–a2+2ad-d2 (1)
Xét tam giác vuông ACH, vận dụng Pytago ta có:
h2=b2–d2(2)
Từ (1) và (2) ta được:
c2–a2+2ad-d2=b2–d2(3)
c2=a2+b2-2ad
Với d = bcos
C:
c2=a2+b2-2abcos
C
Với d = bcos
C vắt vào (3) ta được điều đề nghị chứng minh!
Hệ trái của định lý cos
Cos
A = b2 + c2 – a22bc
Cos
B = c2 + a2 – b22ca
Cos
C = a2 + b2 – c22ab
Hệ quả này có một chân thành và ý nghĩa quan trọng: “Trong một tam giác, ta luôn luôn tính được các góc ví như biết 3 cạnh.”
Vậy trường hợp định lý cosin được cho phép tính những cạnh thì hệ quả của nó chất nhận được tính góc trong tam giác. Có thể áp dụng nó vào một bài toán khá quen thuộc thuộc: “Lập cách làm đường vừa đủ trong tam giác”.
Cách vận dụng định lý cosin trong tam giác
Bài 1: Đường dây cao nỗ lực thẳng trường đoản cú A đến B bao gồm độ nhiều năm 10km, từ bỏ A đến C gồm độ nhiều năm 8km, góc tạo bởi hai tuyến đường dây trên khoảng chừng 75 độ. Tỉnh khoảng cách từ B mang lại C?
Lời giải:
Theo định lý cos ta có:a2=b2+c2-a.b.c.cos
A= 82 + 102 -2.8.10.cos75 122 km
Bài 2: mang lại tam giác ABC tất cả góc A = 120 độ, cạnh b = 8cm cùng c = 5cm. Tính cạnh a với góc B, C?
Lời giải:
Theo định lý cosin ta có:a2=b2+c2-2.b.c.cos
A= 82 + 52 -2.8.5.cos120→ a = 11,4km
B = c+a-b22.a.c → góc B = 37 độ
Góc: A + B + C = 180 độ => góc C = 180° – 120° – 37° = 23 độ
Bài 3: mang lại tam giác ABC tất cả BC = a, CA = b, AB = c và con đường trung con đường AM = c = AB. Chứng tỏ rằng: a2=2(b2+c2)
Lời giải:
Ta có định lý về trung tuyến đường như sau:
AM2=2(AB2+AC2)-BC24
c2=2(c2+b2)-a24
4c2=2c2+2b2–a2
a2=2(b2–c2) (dpcm)
Cũng rất có thể áp dụng định lý hàm số cos để tính tam giác vào thực tế. Có nhiều bài toán yêu mong tính độ cao của một cây cao nào kia hoặc một dự án công trình mà họ không thể trèo lên đỉnh để đo trực tiếp được. Ví dụ, nếu bạn có nhu cầu đo chiều cao của tháp Eiffel, các bạn không thể trèo lên đỉnh của nó và kéo thước dây ra nhằm đo trực tiếp. Sau đó, để đo độ cao của nó, bọn họ sẽ vận dụng định nghĩa của triết lý cosin vào độ nhiều năm tương ứng của những tam giác để tính chiều cao cần thiết.
Xây dựng bí quyết tính con đường trung bình của tam giác theo bố cạnh dựa trên hai luận điểm cơ phiên bản “Muốn tính một cạnh thì phải ghi nhận hai cạnh còn sót lại và góc ngơi nghỉ giữa”, “Muốn tính một góc, bạn phải biết cạnh tương ứng”. Đây cũng chính là hai ý nghĩa quan trọng của định lý cosin cùng hệ quả của nó.
Thế làm sao là hàm số bậc nhất? các dạng bài tập liên quan
Kiến thức ôn thi vào lớp 10 môn toán theo siêng đề – phần 1
Phân thức đại số là gì? bài bác tập vận dụng
Kết luận
THÔNG TIN LIÊN HỆ
Định lý hàm cos – định lý hàm số cos tốt định lý cosin trong tam giác là 1 trong định lý rất quan trọng đặc biệt được áp dụng – ứng dụng rộng thoải mái trong chương trình giáo dục đào tạo đào tạo. Nội dung bài viết dưới đó là kiến thức tổng hợp độc nhất vô nhị về định lý, mời bạn đọc cùng theo dõi!Sự ra đời của định lý hàm cos (định lý cosin)
Định lý Cosin là không ngừng mở rộng của định lý Pythagore. Trường hợp định lý Pythagore cung cấp cho họ một công cụ hiệu quả để search một cạnh không đủ trong một tam giác vuông, thì định lý hàm số Cosin chỉ dẫn một phương thức giúp ta tìm kiếm được một cạnh của tam giác thường khi biết được hai cạnh cùng góc xen thân chúng, các góc của một tam giác lúc biết các cạnh của một tam giác, cạnh thứ ba của một tam giác nếu biết hai cạnh với góc đối của một trong các hai cạnh đó.
Định lý của Euclide
Vào cố kỉnh kỷ III trước công nguyên, tất cả một định lý được phát biểu dưới mẫu mã học vì chưng nhà toán học Euclide chỉ dẫn mà được xem như là tương đương cùng với định lý hàm số Cosin. Định lý của Euclide được tuyên bố như sau:
“Trong một tam giác tù, bình phương của cạnh đối lập góc tù to hơn so với tổng bình phương của của hai cạnh kề góc tội phạm là nhị lần diện tích s của hình chữ nhật gồm một cạnh bằng một trong những hai cạnh kề góc tù của tam giác ( ví dụ là cạnh có đường cao hạ xuống nó ) và đoạn thẳng đã có cắt bớt từ con đường thẳng kéo dãn dài của cạnh kia về phía góc tù bởi đường cao trên.”
Định lý hàm cos vào tam giác
Định lý hàm cos hay (định lý cosin) trong hình học tập Eculid biểu diễn sự liên quan giữa chiều dài những cạnh vào một tam giác phẳng cùng với cosin (hay cos) của góc tương ứng.
Phát biểu định lý cosin
Trong một tam giác phẳng, bình phương một cạnh bởi tổng bình phương nhì cạnh còn sót lại trừ đi nhì lần tích của bọn chúng với cosin của góc xen giữa hai cạnh đó.
Công thức định lý
Xét tam giác phẳng ABC bất kỳ có độ dài những đoạn trực tiếp như sau: BC = a, AC = b, AB = c, những góc tương ứng: góc A = anpha, góc B = beta, góc C = gamma, ta có:
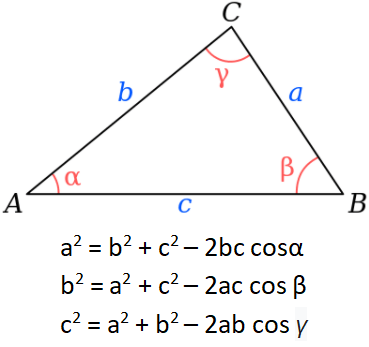
Định lý hàm cos
Nhận xét: trong một tam giác phẳng nếu biết được hai cạnh với góc xen giữa ta và tính được độ lâu năm của cạnh còn sót lại hoặc tính góc lúc biết 3 cạnh của tam giác.
Trường hợp tổng quát của định lý hàm số cos là định lý Pytago. Khám phá kiến thức tổng quan tuyệt nhất về định lý Pytago: TẠI ĐÂY!
Với bí quyết nêu trên, nếu như tam giác ABC vuông ta có:
Tam giác ABC vuông trên A, cos α (hoặc A) = 0 => a2 = b2 + c2Tam giác ABC vuông trên B, cos β (hoặc B) = 0 => b2 = a2 + c2Tam giác ABC vuông tại C, cos γ (hoặc C) = 0 => c2 = a2 + b2Chứng minh định lý cosin
Có nhiều cách để chứng minh định lý rất có thể kể cho nhứ:
Sử dụng bí quyết tính khoảng cáchSử dụng cách làm lượng giác
Sử dụng định lý Pytago
Sử dụng định lý Ptolemy
Ở đây, dễ dàng chứng tỏ nhất ta nên sử dụng định lý Pytago, cách làm sẽ như sau:
Xét tam giác ABC là tam giác nhọn (tam giác gồm 3 góc đều nhỏ hơn 90 độ) tất cả BC = a, AC = b, AB = c, kẻ AH vuông góc cùng với BC trên H; AH = h; HC = d.
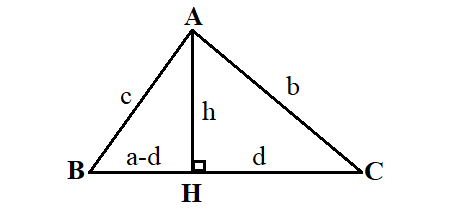
Chứng minh định lý hàm cos
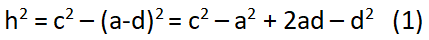
Chứng minh định lý hàm cos – Phương trình 1
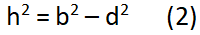
Chứng minh định lý hàm cos – Phương trình 2
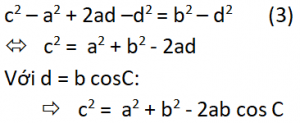
Chứng minh định lý hàm cos – Phương trình 3
Trường phù hợp tam giác phạm nhân (tam giác có một góc to hơn 90 độ) cách minh chứng tương tự.
Hệ quả – vận dụng định lý
Từ bí quyết định lý hàm số cos ta đúc rút được phương pháp tính góc tam giác nhứ sau:
Với ma, mb, mc lần lượt là độ dài trung tuyến kẻ từ bỏ A, B, C, ta gồm công thức tính độ lâu năm trung tuyên như sau:
Với ha, hb, hc thứu tự là độ dài đường cao kẻ từ bỏ A, B, C, ta có một số bí quyết tính diện tích s tam giác như sau:
Bài tập về định lý cosin (định lý hàm cos)
Bài 1: Đường dây cao cầm cố thẳng từ vị trí A đến vị trí B lâu năm 10km, từ vị trí A mang lại vị trí C nhiều năm 8km, góc sinh sản bởi hai đường dây trên khoảng chừng 75° độ. Tính khoảng cách từ địa chỉ B đến vị trí C?
Hướng dẫn giải:
Theo định lý cosin ta có: a² = b² + c² – 2.b.c.cosA = 8² + 10² – 2.8.10.cos75° ≈ 122 km
Vậy khoảng cách từ B mang lại C là 11 km
Bài 2: mang lại tam giác ABC tất cả góc A=120°, cạnh b=8cm và c=5cm. Tính cạnh a và những góc B, C của tam giác đó?
Hướng dẫn giải:
Theo định lý cosin ta có: a² = b² + c² – 2.b.c.cosA = 8² + 5² – 2.8.5.cos120° => a ≈ 11,4 km
Cos
B = (c² + a² – b²) / 2.a.c => góc B ≈ 37° độ
Góc: A + B + C = 180° => góc C = 180° – 120° – 37° = 23° độ
Bài 3: đến tam giác ABC có cạnh BC = a, cạnh CA = b, cạnh AB = c và mặt đường trung con đường AM = c = AB. Chứng tỏ rằng: a² = 2.(b² + c²)?
Hướng dẫn giải:
Theo định lý về trung đường của tam giác ta có: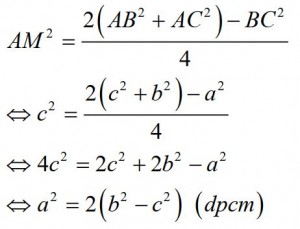
Mục tiêu bài viết
Sau lúc xem hoàn thành bài viết, chúng ta có thể nắm bắt được những kiến thức về:
Liệt kê được những hệ thức lượng trong tam giác.Ứng dụng định lý cosin vào việc giải câu hỏi thực tế.Xem thêm: Đăng Ký Internet Banking Vietinbank Có Mất Phí Không, Biểu Phí Dịch Vụ Ngân Hàng Số
Các kỹ năng:
Giải được đúng đắn các câu hỏi về tam giác ứng dụng định lý cosin.Giải được bài bác toán chứng tỏ các hệ thức về mối liên hệ giữa những yếu tố của một tam giác.Kiến thức tham khảo
Bài viết tham khảo: Tổng hợp cách làm lượng giác
Bài viết tham khảo: Tổng hợp kỹ năng và kiến thức về định lý Talet!
Bài viết tham khảo: Tổng hợp kiến thức và kỹ năng về định lý Pytago!
Bài viết tham khảo: Tổng hợp kỹ năng về định lý Ceva!
Bài viết tham khảo: Tổng hợp kiến thức về định lý Menelaus
Chuyên mục tham khảo: Toán học
Nếu các bạn có bất cứ thắc mắc vui lòng bình luận phía dưới hoặc Liên hệ bọn chúng tôi!