1. Hình elip là gì?
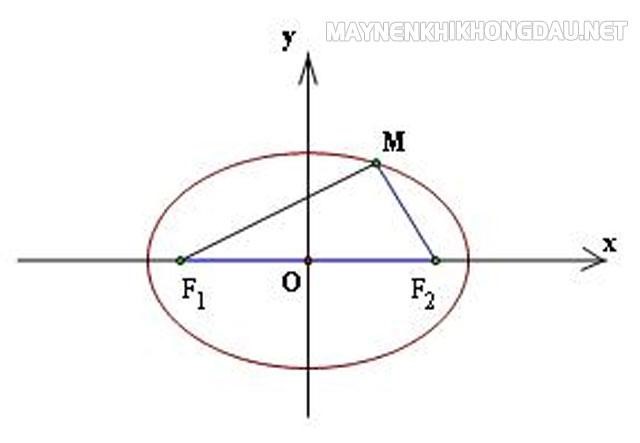
Elip là tập hợp những điểm p. Trong mặt phẳng luôn luôn thỏa mãn: F1P + F2P = 2a (*)

Trong hình trên:
P là một điểm nằm trong hình elip, nó luôn luôn thỏa mãn (*)Hình elip có hai tiêu điểm là F1( – c; 0) và F2( c; 0). Khoảng cách từ F1 cho tới F2 điện thoại tư vấn là tiêu cự: F1F2 = 2c (**)Ta dễ dàng chứng tỏ được b2 = a2 – c2 (***)2. Diện tích s hình elip
Giả sử hình elip có:
độ nhiều năm trụ to AB = 2ađộ dài trục nhỏ tuổi là CD = 2bThì bí quyết tính diện tích s của hình elip là S = π.a.b
3. Phương trình elip
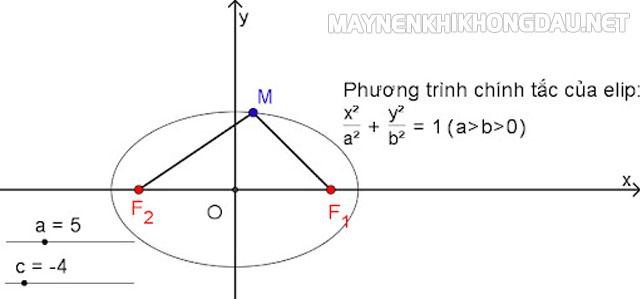
Phương trình elip tổng quát bao gồm dạng:

Trong đó:
độ lâu năm trụ mập AB = 2ađộ lâu năm trục nhỏ dại là CD = 2bkhoảng biện pháp giữ nhì tiêu điểm F1F2 = 2cMối tương tác cần nhớ b2 = a2 – c2
4. Bài bác tập
Bài tập 1. Hãy tính diện tích s hình elip, biết:
a) độ lâu năm trụ bự 6 cm và độ dài trục nhỏ tuổi 4 cm
b) độ nhiều năm trụ béo AB = 4 cm và độ lâu năm trục nhỏ tuổi CD = 3,5 cm
c) Điểm xa tốt nhất nằm bên trên elip giải pháp gốc tọa độ là 5 cm và điểm sớm nhất nằm trên elip phương pháp gốc tọa độ là 4 cm.
Bạn đang xem: Công thức tính chu vi hình elip
Hướng dẫn giải
a) Theo đề
AB = 6 centimet => 2a = 6 cm => a = 3 cm.CD = 4 centimet => 2b = 4 centimet => a = 2 cm.Công thức tính diện tích s hình elip: S = π.a.b = π.3.2 = 6π (cm2)
b) Ta có:
AB = 4 cm => 2a = 4 cm => a = 2 cm.CD = 3,5 cm => 2b = 3,5 centimet => b = 1,75 cm.Công thức tính diện tích s của hình elip: S = π.a.b = π.2.1,75 = 3,5π (cm2)
c) Theo đề:
Điểm xa độc nhất nằm bên trên elip phương pháp gốc tọa độ là a = 5 cmĐiểm gần nhất nằm bên trên elip giải pháp gốc tọa độ là b = 4 cm.
Cách tính diện tích s hình elip theo công thức: S = π.a.b = π.5.4 = 20π (cm2)
Bài tập 2. Hãy viết phương trình elip lúc biết
a) a = 4 cm, b = 3 cm
b) a = 6 cm, c = 5 cm
Hướng dẫn giải
a) Theo đề:
a = 4 cmb = 3 cmPhương trình elip bao gồm dạng:
$fracx^2a^2 + fracy^2b^2 = 1 Leftrightarrow fracx^24^3 + fracy^23^2 = 1 Leftrightarrow fracx^216 + fracy^29 = 1$
b) Theo đề
a = 5 cmc = 3 cm => $b = sqrt a^2 – c^2 = sqrt 5^2 – 3^2 = 4left( cm ight)$Dựa vào biến hóa trên, ta suy ra phương pháp viết phương trình elip là:
$fracx^2a^2 + fracy^2b^2 = 1 Leftrightarrow fracx^25^3 + fracy^24^2 = 1 Leftrightarrow fracx^225 + fracy^216 = 1$
Qua nội dung bài viết này các bạn đã gọi hình elip là gì, cách làm tính chu vi và ăn mặc tích hình elip.
Hình Elip là 1 phần nội dung kỹ năng và kiến thức không thể bỏ qua trong hệ thống hình học tập lớp 10. Bạn đã biết hình elip là gì? giải pháp tính diện tích hình elip ra sao? Phương trình elip như vậy nào?
Vậy mời chúng ta cùng theo dõi nội dung bài viết dưới đây sẽ tổng hợp kỹ năng về phần elip để rất có thể lưu lại với trau dồi cho bạn dạng thân về phần kiến thức và kỹ năng hình học của bậc trung học đa dạng này nhé!
Định nghĩa
Hình Elip là gì?
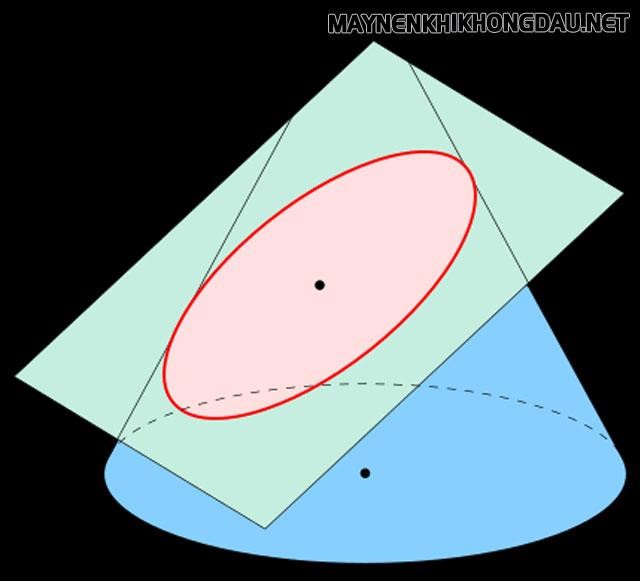
Hình elip hay được định nghĩa là một trong những hình mong dẹt, bao gồm dạng của một hình thai dục. Để dễ hiểu nhất về hình trạng của một hình elip là họ cắt một hình nón có góc to hơn 0.

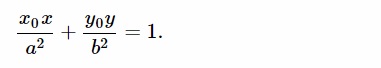
Trong đó:
π là một trong những hằng số toán học có giá trị: π = 3.14159265359
r1, r2 theo lần lượt là độ dài một nửa của trục lớn và trục nhỏ.
Bài tập áp dụng kỹ năng về hình Elip
Bài 1: Tính diện tích s hình elip, biết:
Trục phệ và trục nhỏ dại có độ lâu năm lần lượt là 8cm và 4cm.Trục lớn MN= 4cm, trục bé dại IK = 2.5cmKhoảng biện pháp từ điểm xa độc nhất nằm trên elip đến gốc tọa độ là 7cm và khoảng cách từ điểm gần nhất nằm trên cho gốc tọa độ là 6cm.
Hướng dẫn phương pháp giải:
a). Tạm hotline trục mập và trục nhỏ tuổi của elip là AB với CD. Theo đề bài xích ta có:
AB = 8cm => 2a = 8cm => a = 4cm
CD = 4cm => 2b = 4cm => b = 2cm
Như vậy, diện tích hình elip là: S = π.a.b = π.4.2 = 8π (cm²).
Xem thêm: Xin zhao mùa 13: bảng ngọc, cách lên đồ xin zhao rừng phút 20 solo baron
b). MN = 4cm => 2a = 4cm => a = 2cm
IK = 2,5cm => 2b = 2,5cm => b = 1,25cm
Diện tích hình elip là: S = π.a.b = π.2.1,25 = 2,5π (cm²)
c). Theo đề bài xích ta có:
Khoảng cách từ điểm xa nhất nằm trên elip cho gốc tọa độ là 7cm => a = 7cm
Khoảng giải pháp từ điểm gần nhất nằm trên elip cho gốc tọa độ là 6cm => b = 6cm
Vậy, diện tích s elip là: S = π.a.b = π.7.6 = 42π (cm²)
Bài 2: Lập phương trình thiết yếu tắc của elip (E) trong số trường hòa hợp dưới đây:
Một đỉnh trên trục béo là (3; 0) cùng một tiêu điểm là (-2; 0)(E) đi qua điểm: M(0; 1) với N(1, √3/2)Hướng dẫn phương pháp giải:
a). Ta có: a = 3, c =2 => b² = a² – c²=9 – 4 =5
Vậy phương trình chính tắc của elip là: x²⁄9 + y²⁄5 = 1
b). Phương trình chính tắc của (E) bao gồm dạng: x²⁄a² + y²⁄b²= 1
Vì (E) đi qua 2 điểm M(0;1) cùng N(1, √3⁄2) đề xuất thay tọa độ của M cùng N vào phương trình (E) ta được:
Vậy, phương trình của hình elip (E) bao gồm dạng: x²⁄4 + y²⁄1 = 1
Chúng ta vừa tổng vừa lòng lại những kỹ năng và kiến thức cơ bản về hình elip cùng áp dụng làm bài xích tập. shthcm.edu.vn hy vọng những thông tin trên hữu ích đối với bạn.